本帖最後由 mca 於 2010-7-18 12:42 編輯
(以下是我知道的故事)
牛頓怎樣發現萬有引力定律
----------------------------------
講野史,坊間往往加鹽加醋來吸引聽眾,中國有康熙遺詔被改寫為 "傳位于四子" 的傳聞,外國亦有牛頓因蘋果跌在頭上而發現萬有引力的故事,現在史學家已証明這些野史不確。
早在青年時代,牛頓已從前輩 Galileo (b 1564)、Kepler (b 1571)、Descartes (b 1596)、Huygens (b 1629)、Hooke (b 1635) 等學者領悟到太陽行星及衛星之間存着某種力量關係 *,這種關係稱為 引力 gravitation,原字出自拉丁語 gravitatem (nom. gravitas),表示「重」的意思。踏入微積分萌芽時代,牛頓更從數學上了解某些參數之間存着 "逆平方律" (inverse square law) 的關係,例如 x = 1 / y^2,於是他開始憧想 ----- 引力與距離是否也有 "逆平方律" 的關係呢? 要知答案,自然要用事實求証,可是一時間牛頓還沒有找到事實証明。
1665 至 1666 年,英國爆發瘟疫,牛頓剛剛大學畢業,他走回 Lincolnshire 鄉間母親處避開瘟疫,某天他偶然在庭園見蘋果從樹上跌下來 **,他靈機一觸就這樣想 ----- 蘋果墜落地上的力 (重量) 與 維持月球繞地球運行之力 (引力) 是否同出一轍呢 ? 究竟這所謂 "引力" 有沒有延展性令其他行星繞太陽運轉 ? 於是他開始計算,當時他大約知道地球半徑 R = 4000 哩 (6400 km),月地距離 D = 240 000 哩 = 60 倍地球半徑,蘋果跌向地面的加速度 a = 32.2 呎/秒/秒 (980 cm/sec^2),因此在頭一秒 ( t = 1 sec) 時,蘋果已下跌了 1/2.a.t.t = 16.1 呎,如果蘋果下墜之力與月地間的引力都是同一力量,而引力又與距離平方成反比的話,那麼月球也應像蘋果在軌道切線之下跌了 16.1 呎 / 60 的平方 = 0.0537 吋,見圖一。
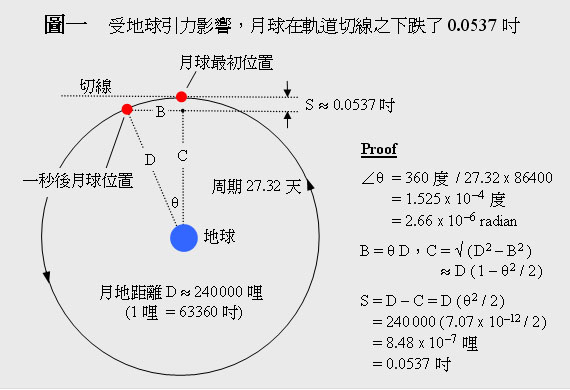
本來像圖一要証明月球下墜 0.0537 吋是很普通的算術,但不知何故,牛頓竟然計錯數 (他把地球半徑的哩數換算為錯誤的吋數,另一說他引用了欠準的地球半徑值),結果他得不到應有的 0.0537 吋,他只好把引力問題放下而轉研其他項目,就這樣一放之下便過了六七年,直至某次他聽到 Picard 發表新的地球半徑數據,於是他重新計算以前的月球/蘋果引力問題,今次他真的計得 ~ 0.0537 吋,說明了三個原理: (一) 蘋果下墜之力與維持月球軌道運動之力是同一性質的 (universal);(二) 兩件物體之間的引力與其距離的平方成反比;(三) 地球上的引力加速度與下墜體的質量無關 (即解釋了伽利略在比蕯斜塔做的跌球實驗)。自此之後牛頓對研究更具信心,友人哈雷 (預測彗星回歸的 Halley) 又鼓勵和資助他發表研究結果,終於在 1687 年出版了影響後世的 Principia ***,1713 年出第二版,1726 年出第三版,今天還有 "網上版"。

--------------------
註 * The Oxford Guide to the History of Physics and Astronomy, page 227:
"In 1679, Newton learned of Robert Hooke's 胡克 idea that orbital or curved motion could be explained by a combination of a linear inertial component along the orbit's tangent and a continual falling inward toward the center. Newton wrote that he had never before heard of this 'hypothesis.' But he perceived a connection between Hooke's suggestion and Johannes Kepler's law of areas .....".
註 ** http://www.maths.tcd.ie/pub/Hist ... Ball/RB_Newton.html
In the year 1666 he retired again from Cambridge ... to his mother in Lincolnshire & while he was musing in a garden it came into his thought that the power of gravity (which brought an apple from a tree to the ground) was not limited to a certain distance from earth, but that this power must extend much further than was usually thought. Why not as high as the Moon thought he to himself & that if so, that must influence her motion & perhaps retain her in her orbit, whereupon he fell a-calculating what would be the effect of that superposition... (Keesing, R.G., The History of Newton's apple tree, Contemporary Physics, 39, 377-91, 1998)
另一網頁 http://www-groups.dcs.st-and.ac.uk/~history/PrintHT/Orbits.html 這樣寫:
Fifty years after these events Newton was to record his own recollections of these events which, although interesting, do not really agree with the known historical facts! [I preserve Newton's old English. Note that ye = the, orb = orbit, wch = which.]
"..... In the same year I began to think of gravity extending to ye orb of the Moon and (having found out how to estimate the force with wch globe revolving within a sphere presses the surface of a sphere) from Kepler's rule of the periodical times of the Planets being in sesquialternate proportion to their distances from the centres of their Orbs, I deduced that the forces wch keep the Planets in their Orbs must reciprocally as the squares of their distances from the centres about wch they revolve: and thereby compared the force requisite to keep the Moon in her Orb with the force of gravity at the surface of the Earth, and found them answer pretty nearly. All this was in the two plague years of 1665-1666....."
註 *** http://www.laughtergenealogy.com/bin/histprof/misc/newton.html
The Principia ----- Newton concluded his first investigations on gravity and motion in 1665 and 1666. Nothing was heard of them for nearly 20 years. His original theory had been based on an inaccurate measurement of the earth's radius, and Newton realized differences between the theory and the facts. Although he later learned the true value of the earth's size, he was not led to complete his investigation or to produce a book for publication.
One day in 1684, Edmond Halley, an English astronomer, Robert Hooke, an English scientist, and Christopher Wren, the architect, were discussing what law of force produced the visible motion of the planets around the sun. They could not solve this problem. Halley went to Cambridge to ask Newton about it. He found Newton in possession of complete proof of the law of gravity. Halley persuaded Newton to publish his findings. Halley paid all the expenses, corrected the proofs, and laid aside his own work to publish Newton's discoveries. Newton's discoveries on the laws of motion and theories of gravitation were published in 1687 in Philosophiae Naturalis Principia Mathematica (Mathematical Principles of Natural Philosophy). This work, usually called Principia or Principia Mathematica, is considered one of the greatest single contributions in the history of science. It includes Newton's laws of motion and theory of gravitation. It was the first book to contain a unified system of scientific principles explaining what happens on earth and in the heavens.
其他參考:
Cambridge Illustrated History of Astronomy, Chapter 6 --- Newton and Newtonianism
On-line versions of Newton’s Principia http://en.wikipedia.org/wiki/Phi ... incipia_Mathematica
Newton might have known gravity from a visible comet, not a falling apple !
http://www.youtube.com/watch?v=D5BQkdyAw8A&feature=related |